Home | Abstract | Intro | Page 1 | Page 2 | Results | Conclusions | References | Acknowledgements
Methods:
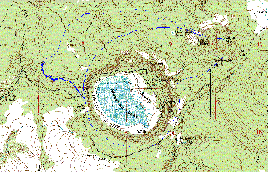
Two major basins were delineated by analysis of
the U.S.G.S. 7.5 minute Topographic Quad Sheet (Stoneman Lake) in
AutoCAD. The two major basins, the
CCC ditch, and an existing bridge are delineated in Figure
A. These two basins were then
subdivided into ten sub-basins according to topographic lines and flow paths (Figure
B). Major Basin 1 is comprised
of sub-basins 1-7 and Major Basin 2 is subdivided into sub-basins 8-10.
The area of each Sub-basin was calculated with AutoCAD.
Table 1 - Sub-basin Areas
|
Sub-basin |
Area
(acres) |
Area |
|
1 |
68.6 |
0.107 |
|
2 |
103 |
0.161 |
|
3 |
164 |
0.257 |
|
4 |
32.4 |
0.0506 |
|
5 |
138 |
0.215 |
|
6 |
123 |
0.192 |
|
7 |
148 |
0.232 |
|
Lake |
134 |
0.210 |
|
8 |
178 |
0.278 |
|
9 |
103 |
0.160 |
|
10 |
42.7 |
0.0667 |
The ditch was surveyed using a Brunton MNS Global Positioning System (GPS) unit, with version 2.01 software, in order to determine latitude and longitude coordinates. Accuracy was +/- 5 meters in the x-y direction, when differentially corrected4. Altitude was not measured. The AllTopo maps program was used to plot ditch coordinates and watershed boundaries. The ditch is outlined by a series of lat-long coordinates that were entered into a table, and watershed boundaries were drawn roughly by hand. The plot is delineated in Figure C:
Figure C - Ditch Coordinate Plot
Cross sectional measurements of the ditch were taken upstream of the bridge (see Figure A) using a level, rod, and measuring tape. In addition, slope was measured at 200-400 foot intervals, and linearly interpolated to determine the slope at each cross section. The thalweg beneath the bridge served as the z-datum reference point. Table 2 depicts slope of the ditch:
Table 2 – Slope of the
Ditch
|
Cross
Section |
Upstream
Distance |
Rise |
Slope |
|
|
ft |
ft |
|
|
Below
Bridge |
-3.0 |
0 |
0 |
|
Bridge |
0.0 |
0 |
0 |
|
3 |
271.8 |
1.40 |
0.0052 |
|
4 |
383.5 |
1.98 |
0.0052 |
|
5 |
690.0 |
4.71 |
0.0068 |
|
6 |
1031.5 |
8.06 |
0.0078 |
|
7 |
1433.0 |
12.00 |
0.0084 |
|
8 |
1674.0 |
14.26 |
0.0085 |
|
9 |
1880.0 |
16.05 |
0.0085 |
|
10 |
2134.3 |
18.71 |
0.0088 |
|
11 |
2314.5 |
20.44 |
0.0088 |
|
12 |
2619.2 |
22.96 |
0.0088 |
|
13 |
2945.1 |
26.16 |
0.0089 |
|
14 |
3264.5 |
28.36 |
0.0087 |
|
15 |
3425.0 |
31.27 |
0.0091 |
Over a distance of 3425 feet, total elevation change was 31.27 feet. This gives the ditch an average slope of about 0.85%. Cross Sectional dimensions were adjusted in elevation based on a linearly interpolated slope, for input into HEC-RAS. This data is found in Table 3. Meander was not measured.
HEC-RAS Analysis
Manning’s roughness coefficients were determined by examination of channel morphology (see examples below):
Figure D: Examples of Channel Morphology
A Manning’s roughness of 0.04 for the channel
and 0.05 for the banks was used based on Chow5 for:
Adjusted Cross Sectional data was entered into HEC-RAS to determine maximum ditch flow capacity, with bank-full height based on the Cross Sections that had the lowest vertical banks (theoretically the first to overflow). A flow of 45 cubic feet per second allowed Cross Sections 12 and 13 to be filled to capacity. Plots of the Cross Sections can be seen in Figure E. The bridge was 3 feet at its deepest point, and is shown in Figure F. Flow could potentially be constricted here, if the ditch were upgraded to increase conveyance.
Figure F – Bridge constriction of the ditch

The following data was calculated by HEC-RAS, and is displayed in Table 4:
Table 4 - HEC-RAS Output
| Cross Section |
Distance (upstream) |
Q
Total |
Wetted |
Water |
Critical |
Energy |
Energy |
Velocity |
Flow |
Top
Width |
|
|
ft |
cfs |
ft |
ft |
ft |
ft |
ft/ft |
ft/s |
ft2 |
ft |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
3425.0 |
45 |
10.96 |
32.47 |
32.47 |
32.89 |
0.027 |
5.19 |
8.67 |
10.54 |
|
14 |
3264.5 |
45 |
15.08 |
29.98 |
29.39 |
30.09 |
0.005 |
2.68 |
16.79 |
14.48 |
|
13 |
2945.1 |
45 |
15.38 |
27.30 |
27.18 |
27.55 |
0.017 |
3.98 |
11.30 |
15.13 |
|
12 |
2619.2 |
45 |
18.43 |
24.84 |
24.30 |
24.93 |
0.005 |
2.49 |
18.10 |
18.02 |
|
11 |
2314.5 |
45 |
10.94 |
21.86 |
21.81 |
22.24 |
0.023 |
4.95 |
9.09 |
10.46 |
|
10 |
2134.3 |
45 |
14.65 |
20.26 |
19.76 |
20.39 |
0.006 |
2.91 |
15.46 |
14.08 |
|
9 |
1880.0 |
45 |
9.55 |
17.57 |
17.44 |
17.94 |
0.019 |
4.93 |
9.13 |
8.77 |
|
8 |
1674.0 |
45 |
14.88 |
15.90 |
15.40 |
16.03 |
0.005 |
2.85 |
15.78 |
14.25 |
|
7 |
1433.0 |
45 |
12.35 |
13.39 |
13.31 |
13.72 |
0.020 |
4.57 |
9.85 |
11.99 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Average |
|
|
13.58 |
|
|
|
|
|
12.68 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1031.5 |
45 |
15.42 |
9.83 |
9.30 |
9.95 |
0.005 |
2.79 |
16.13 |
14.91 |
|
5 |
690.0 |
45 |
12.98 |
6.05 |
6.05 |
6.42 |
0.028 |
4.90 |
9.19 |
12.68 |
|
4 |
383.5 |
45 |
15.25 |
3.75 |
3.09 |
3.85 |
0.004 |
2.55 |
17.62 |
14.59 |
|
3 |
271.8 |
45 |
12.81 |
3.10 |
2.66 |
3.27 |
0.007 |
3.29 |
13.69 |
12.15 |
|
2 |
0.0 |
45 |
14.93 |
1.61 |
1.01 |
1.72 |
0.005 |
2.71 |
16.58 |
13.57 |
|
1 |
-3.0 |
45 |
10.55 |
1.23 |
1.23 |
1.66 |
0.027 |
5.26 |
8.55 |
10.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Average (Above
Bridge) |
|
|
13.66 |
|
|
|
|
|
13.63 |
|
Flow path Analysis
Theoretical flow paths were defined based on topographic features. A few possible flow paths were drawn for each sub-basin and measured in AutoCAD. Each path was then divided into reaches of sheet flow, shallow concentrated flow and open channel flow. Sheet flow comprises the first 300 feet of flow from the farthest-most point in the watershed. The segment between sheet flow and channel flow is designated as shallow concentrated flow. Channelized flow was estimated to occur where contour lines became pointed, indicating a channelized drainage6. Possible flow paths are depicted in Figure G.
The longest flow paths available for each watershed were used to determine runoff travel time for each basin. These flow paths are depicted in Figure H. The ditch was subdivided into 2 parts to allow for the fact that drainage into the ditch occurs at two central points from Sub-basins 8 and 10. Sub-basin drainage parameters are provided in Table 5.
Table 5 - Flow Path Length and Slope
| Sub-basin |
Sheet Length ft |
Sheet Slope |
Shallow Concentrated Length ft |
Shallow Concentrated Slope |
Channel Flow Length ft |
Channel Slope |
| 1 | 300 | 0.02 | 642 | 0.11 | 2492 | 0.16 |
| 2 | 300 | 0.04 | 604 | 0.08 | 2315 | 0.23 |
| 3 | 300 | 0.13 | 2494 | 0.06 | 2851 | 0.20 |
| 4 | 0 | - | 0 | - | 2545 | 0.16 |
| 5 | 300 | 0.23 | 713 | 0.34 | 2792 | 0.14 |
| 6* | 716 | 0.11 | 958 | 0.34 | 0 | - |
| 7* | 348 | 0.14 | 512 | 0.33 | 0 | - |
| 8 | 0 | - | 0 | - | 4018 | 0.03 |
| 9 | 300 | 0.17 | 2847 | 0.07 | 3585 | 0.07 |
| 10 | 300 | 0.10 | 1474 | 0.07 | 1258 | 0.06 |
| Ditch 1 | 0 | - | 0 | - | 2776 | 0.007 |
| Ditch 2 | 0 | - | 0 | - | 989 | 0.012 |
Time of concentration (Tt) was calculated using the TR-55 calculator in Stormwater Management and Design Aid (SMADA) version, 6.437.
This calculator is based on the Natural Resource Conservation Service TR-55 method8 where:
Sheet Flow:
| Ts | = | 0.007 |
(nL)
0.8 |
|
|
|||
|
(P2)0.5 (So) 0.4 |
Where:
| Ts | = | travel time in hours | |
| n | = | Manning's roughness coefficient for overland flow | |
| L | = | flow length, feet | |
| P2 | = | two year 24-hour rainfall, inches | |
| So | = | land slope |
Shallow Concentrated Flow:
| Tsc | = | Lsc |
|
|
||
| 3600Vsc |
Where
| Tsc | = | travel time in hours | |
| Lsc | = | flow length, feet | |
| Vsc | = | Velocity (ft/s) based on slope, See Figure I |
Figure I
Channel Flow:
| Vch | = | 1.49 | (R)2/3 (So) 1/2 |
|
|
|||
| n |
Where:
| Vch | = | Velocity of the channel, feet/s |
|
| n | = | Manning's roughness coefficient for overland flow | |
| R | = | Hydraulic Radius, feet | |
| So | = | land slope |
The
Manning’s n was estimated to be 0.05. Because R is a necessary input, a
theoretical value was calculated using a
trapezoidal channel with a 100:1 horizontal to vertical ratio and a bottom width
of 3 feet . R resulted in a value
of 0.27 feet.
| Tch | = | L |
|
|
||
| 3600Vch |
| Tch | = | travel time in hours | |
| L | = | length, feet | |
| Vch | = | Velocity, feet/s |
Ts, Tsc and Tch are then summed to give a total Time of concentration, Tt. Lag time (Tl) is defined as 0.6* Tt, and will be used in the HEC-HMS model.
Table 6 - Sub-basin Lag Times
|
Sub-Basin |
Tt |
Tl |
Tl |
|
|
hours |
hours |
minutes |
|
1 |
1.08 |
0.648 |
38.9 |
|
2 |
0.833 |
0.500 |
30.0 |
|
3 |
0.731 |
0.439 |
26.3 |
|
4 |
0.113 |
0.068 |
4.07 |
|
5 |
0.552 |
0.331 |
19.9 |
|
6* |
0.064 |
0.038 |
2.30 |
|
7* |
0.032 |
0.019 |
1.15 |
|
8 |
0.412 |
0.247 |
14.8 |
|
9 |
0.828 |
0.497 |
29.8 |
|
10 |
0.682 |
0.409 |
24.6 |
|
Ditch
1 |
0.291 |
0.175 |
10.5 |
|
Ditch
2 |
0.076 |
0.046 |
2.74 |
*Times for Sub-basins 6 and 7 were calculated
using 2 reaches of shallow concentrated flow.
The Soil Conservation Service method was used for
Input Losses and Rate Transformation8.
The SCS method is based on the assumption that:
| Q | = | (P - Ia)2 | Where P>Ia | |
|
|
||||
| (P - Ia) + S |
| S | = | potential maximum retention | |
| Q | = | runoff | |
| P | = | precipitation | |
| Ia | = | initial abstraction |
and
| Curve Number | = | 1000 | |
|
|
|||
| 10 + 0.0394S |
Because I have no actual rainfall-runoff calibration for this watershed, SCS curve numbers will be estimated from an adjacent watershed with similar groundcover. In the Oak Creek Flood Warning System Hydrology Report9, curve numbers are calculated for vegetation and geology that are very similar to the Stoneman Lake watersheds. Curve numbers are based on all Hydrologic Soil Groups – A, B, C and D.
The Environmental Protection Agency (EPA) has downloadable soil coverage values for all 50 states10. The area of interest contains type B or type D soils, therefore, I chose the intermediate type of C for calculating final runoff. The Oak Creek study provides a curve number of 65 for Ponderosa Pine, Fair Cover Condition (30-70%), and type C soils.
Home | Abstract | Intro | Page 1 | Page 2 | Results | Conclusions | References | Acknowledgements